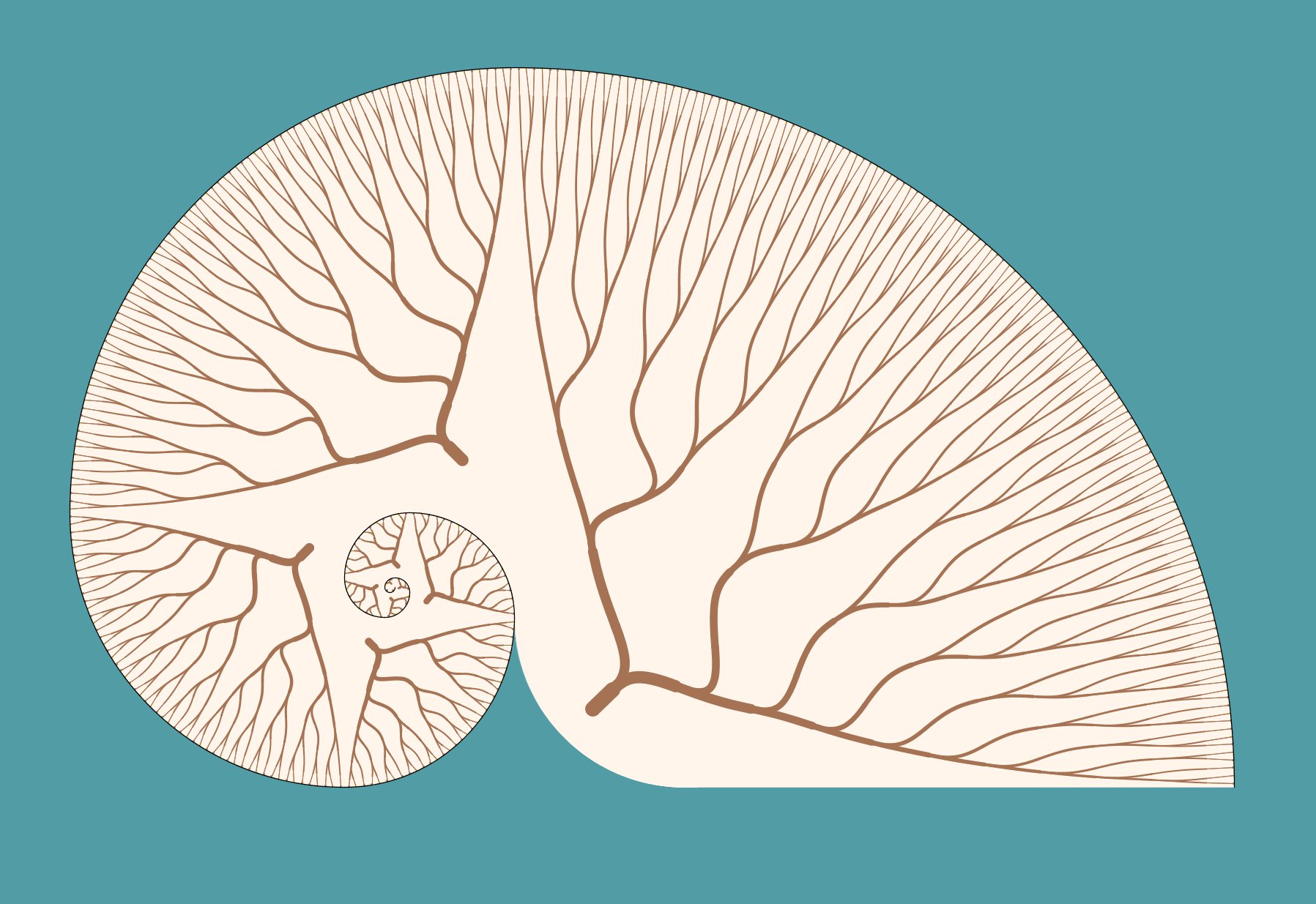
This work is a combination of Fibonacci elements in a shell-like pattern similar to a nautilus. Twelve quarter-circle sectors are used to create the shell. Each sector is patterned with a tree showing the generational pattern used to create the Fibonacci numbers.
Background and Inspiration
Named in honor of Leonardo of Pisa (Fibonacci), the Fibonacci sequence arises from a problem stated in his book on arithmetic Liber Acci (1202), but knowledge of the sequence dates back over 2000 years in India. The problem Fibonacci posed is this: given a pair (male and female) of newborn rabbits. Rabbits reach reproductive maturity after one month and produce another pair (male and female) at the end of the second month. Assuming this pattern continues with no deaths, how many pairs of rabbits will there be after one year?
The sequence starts with 0 and 1, then successive terms are obtained by adding together the previous two. This generates the sequence \[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, \ldots\] Thus, the Fibonacci sequence is given by the recurrence relationship \[ F_0 = 0,\ F_1 = 1,\ \text{and}\ F_n = F_{n-1} + F_{n-2} \ \text{for}\ n \ge 2. \] Interestingly, \[\lim_{n\to\infty} \frac{F_n}{F_{n-1}} = \varphi = \frac{1 + \sqrt{5}}{2} = 1.61803\ldots,\] where \(\varphi\) is the golden ratio.
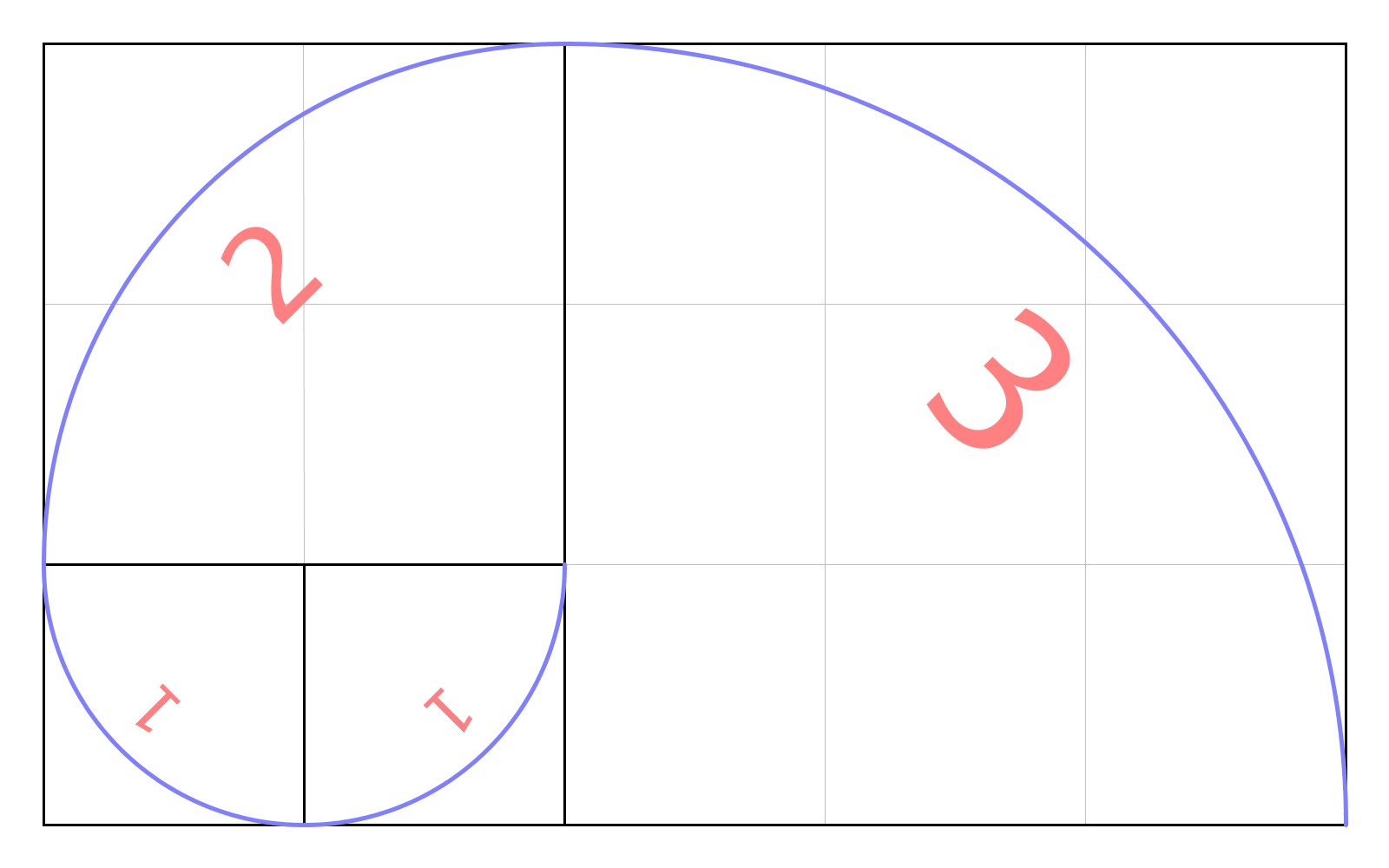
The Fibonacci sequence can be used to generate a spiral
form
made from quarter circle arcs.
The arcs are not only continuous, but have the same tangent where they meet,
so they appear to be smoothly connected even though they are piecewise defined.
This process is shown for the first 4 non-zero sequence values and
can be continued for the remaining values of the sequence.
The branching pattern seen in each quarter circle reflects the population growth. At each bifurcation, the number of endpoints on either side are successive Fibonacci numbers. After each bifurcation, the mature pair continues on the clockwise direction. The delay in rabbit maturity of the new pair is reflected in the delay in bifurcation on the counter-clockwise side.
Exhibition History
- Mathematics as Muse, Ella Sharp Museum, Jackson, Michigan. 1-31 October 2016.
- Mathematical Art Exhibition, Joint Mathematics Meetings, Baltimore, Maryland. 15–18 January 2015.
- Bridges 2014 Exhibition of Mathematical Art, Seoul, Korea. 14-19 August 2014.
Publication History
- 2014 Joint Mathematics Meetings Exhibition of Mathematical Art, p. 91, Edited by Robert Fathauer and Nathan Selikoff, ISBN: 978-1-938664-09-0, Tessellations Publishing, 2014.
- Bridges Seoul Art Exhibition Catalog, p. 104, Edited by Conan Chadbourne, Robert Fathauer, and Katie McCallum, ISBN: 978-1-938664-12-0, Tessellations Publishing, 2014.